—
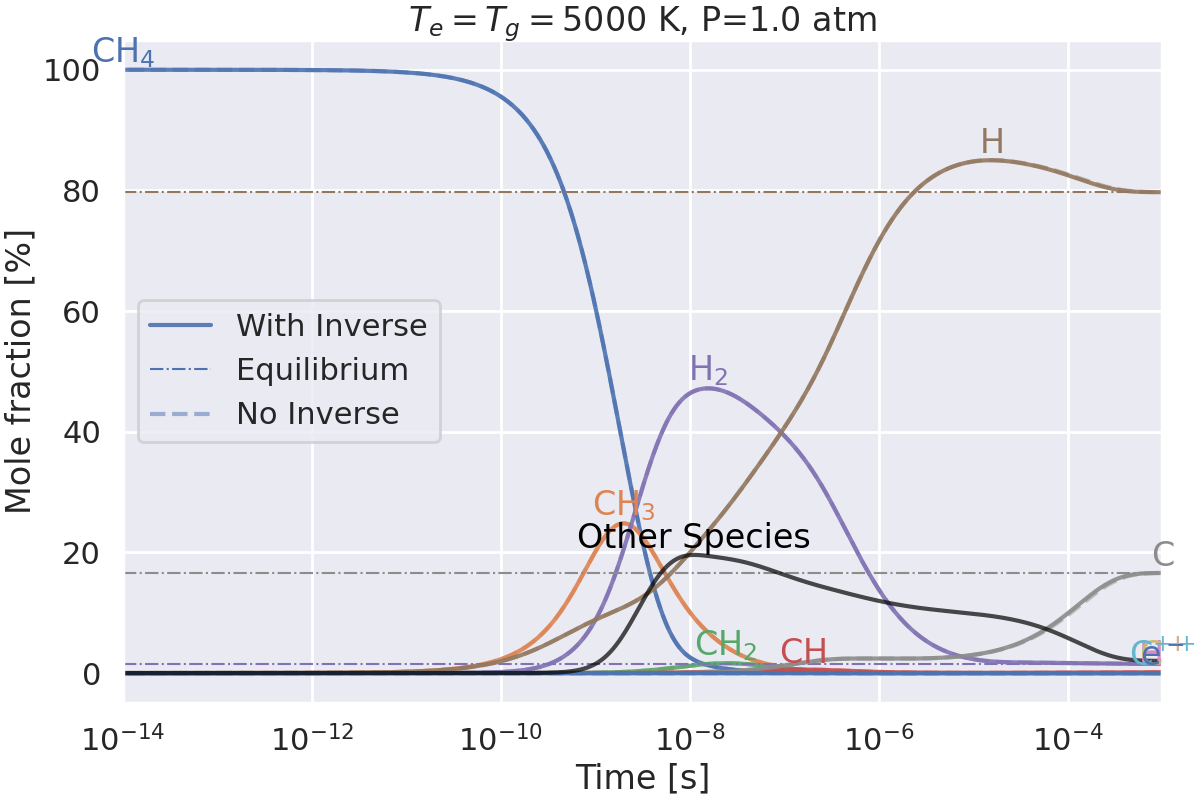
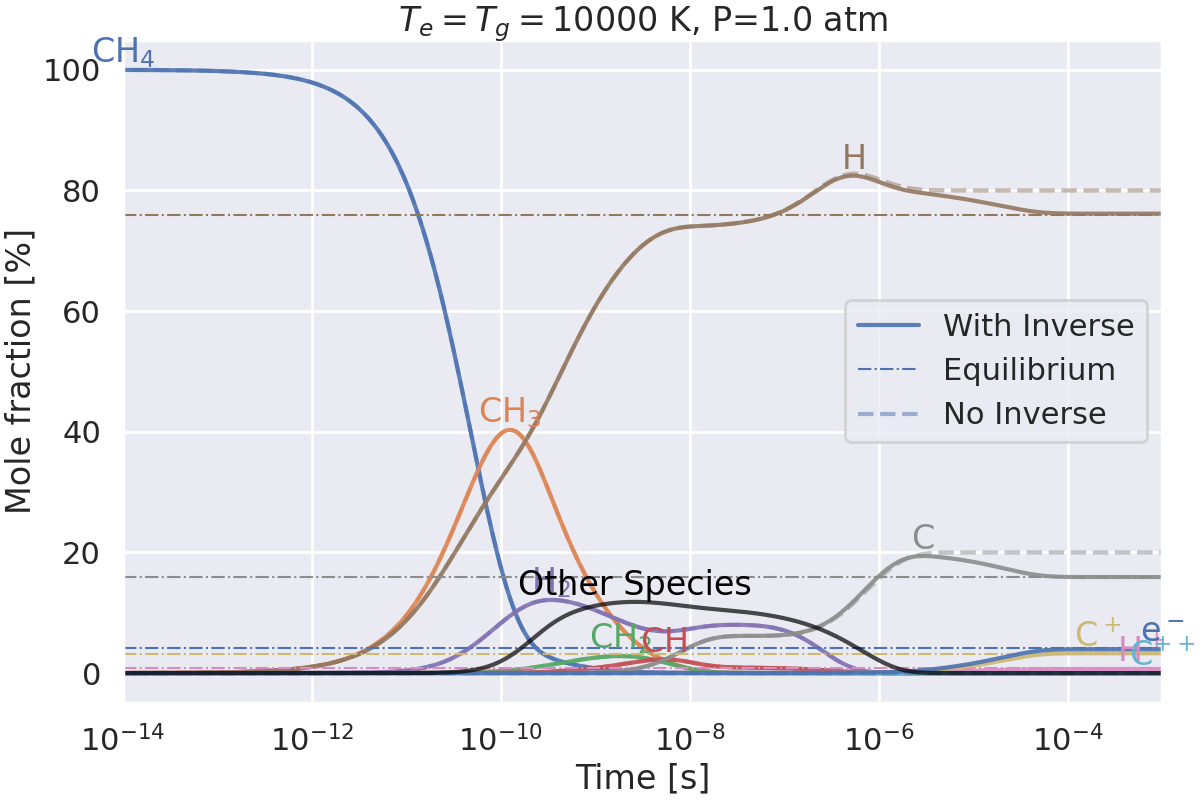
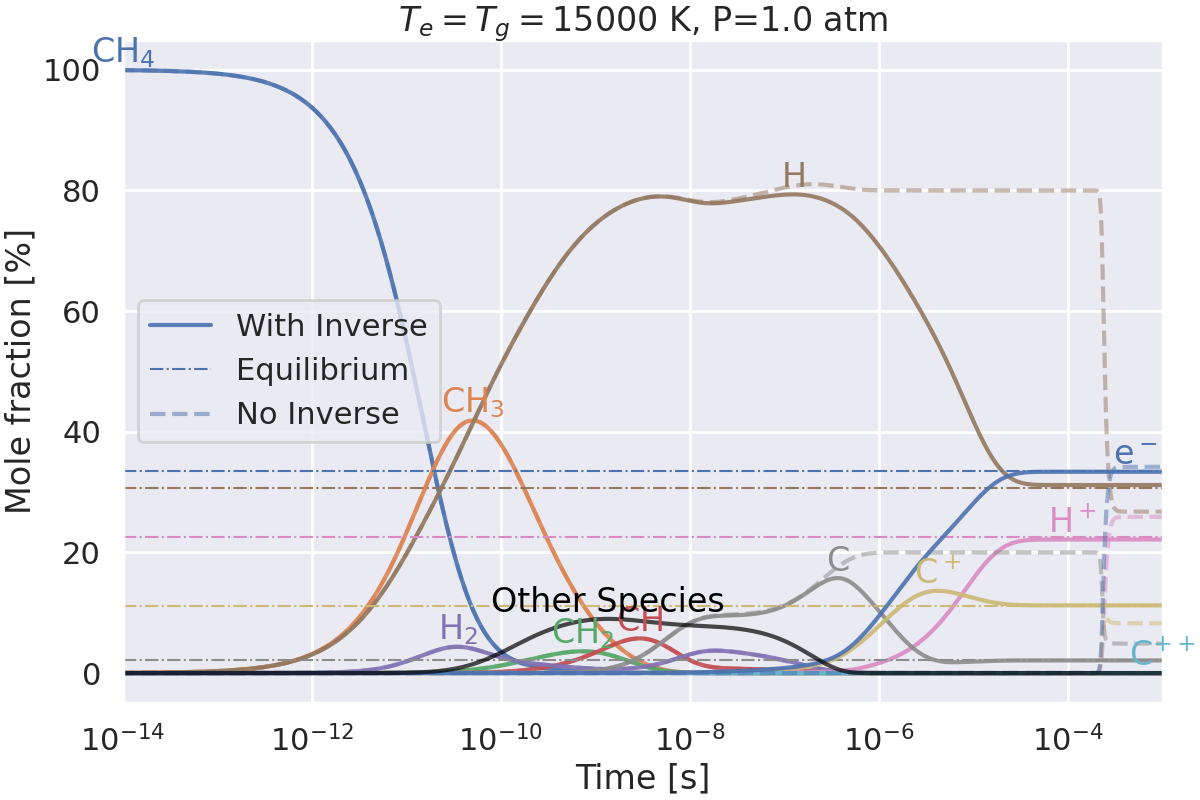
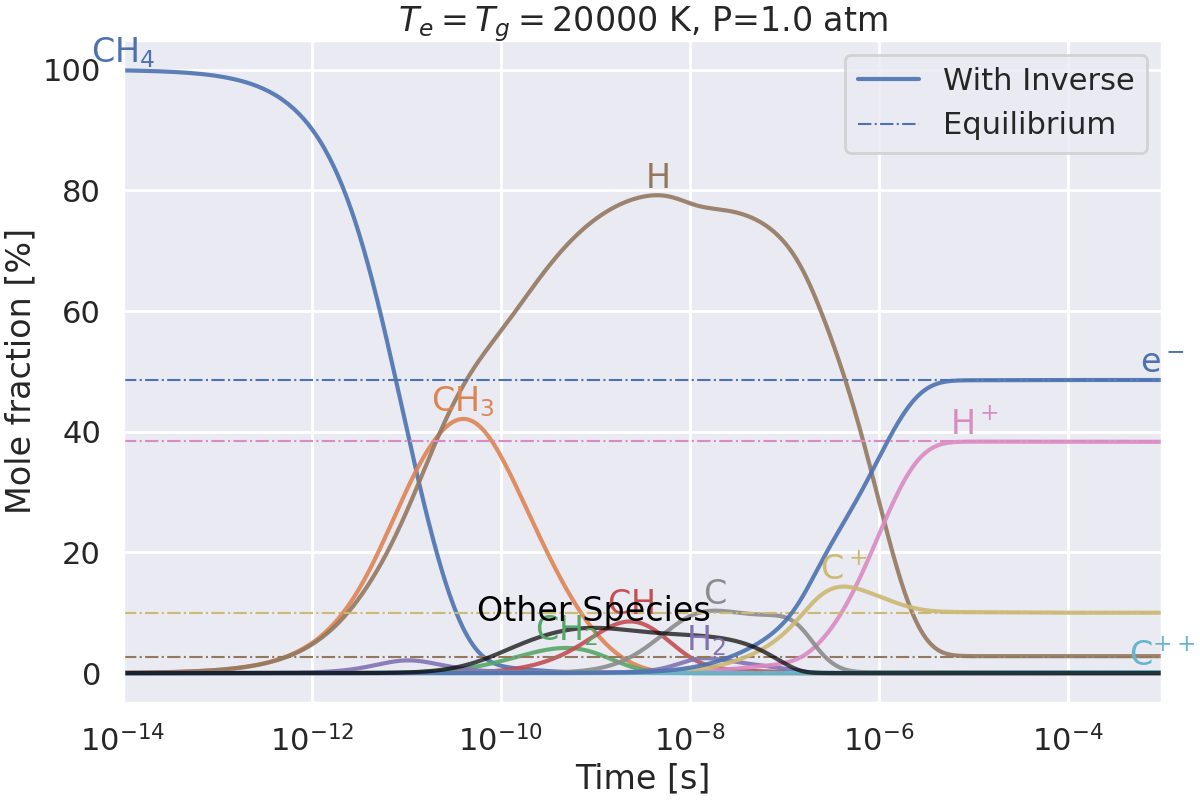
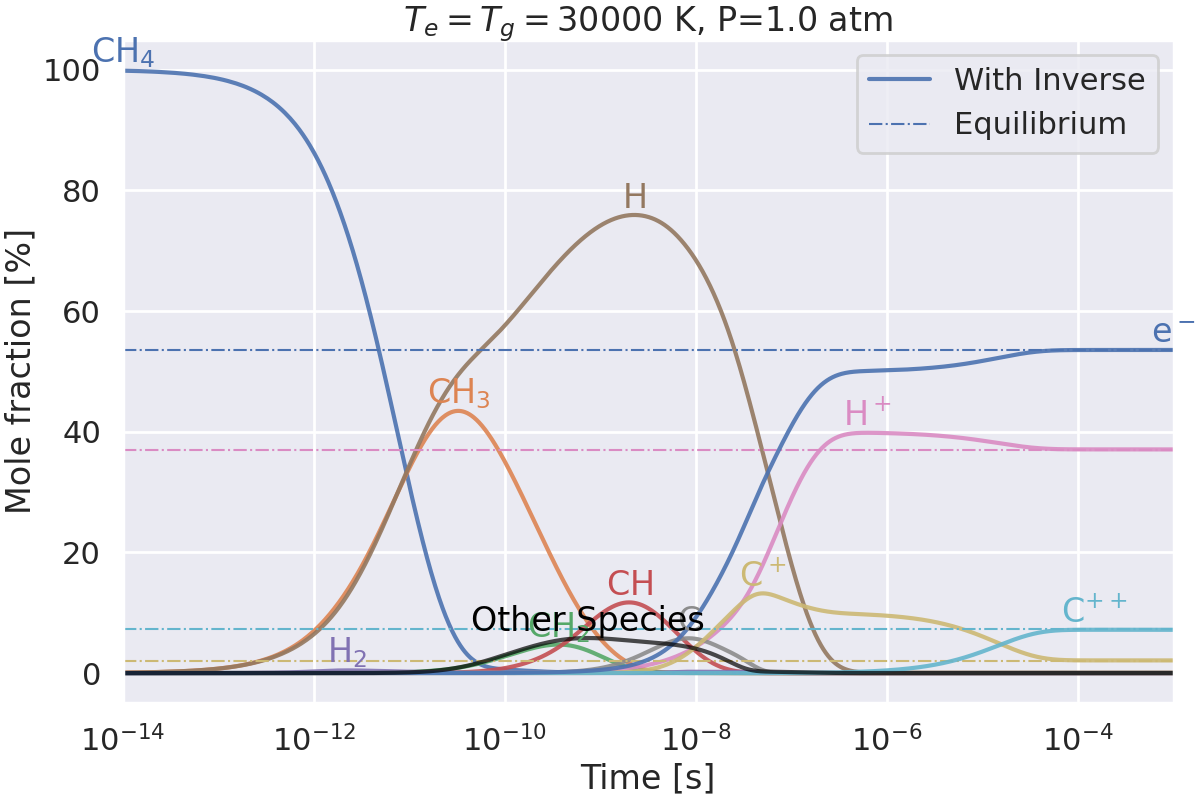
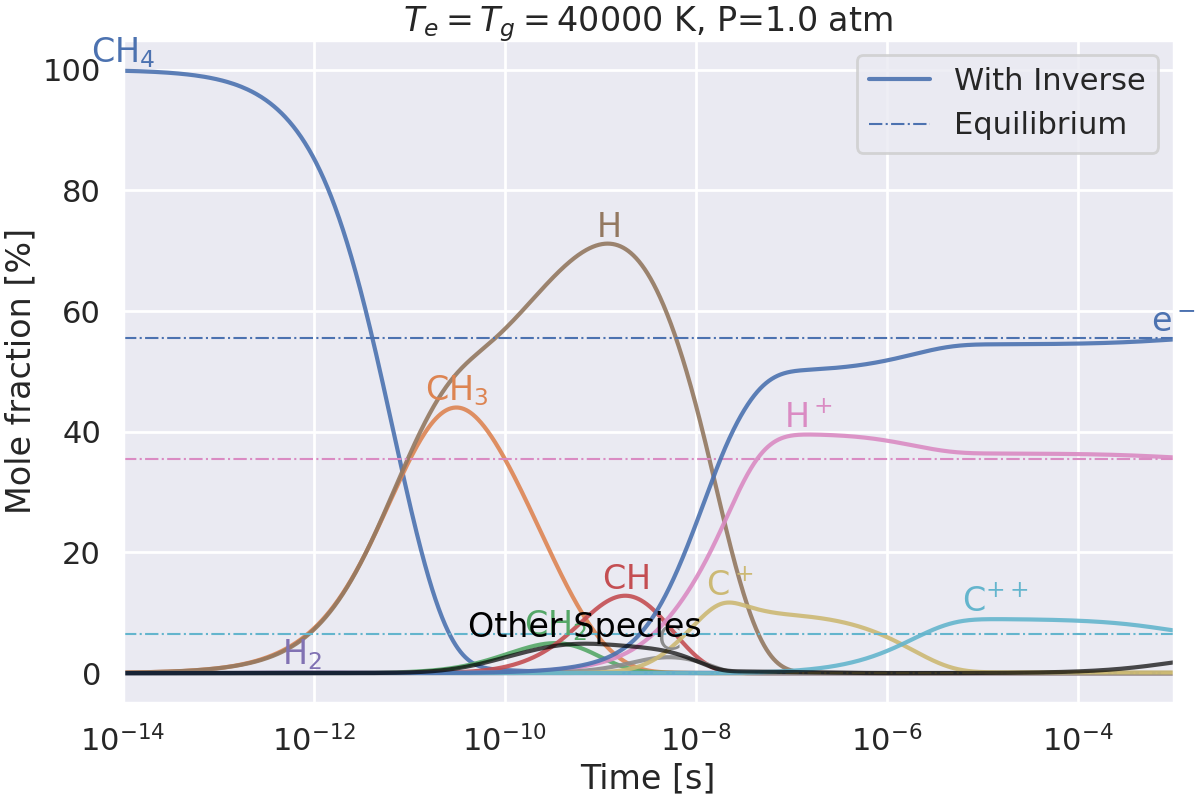
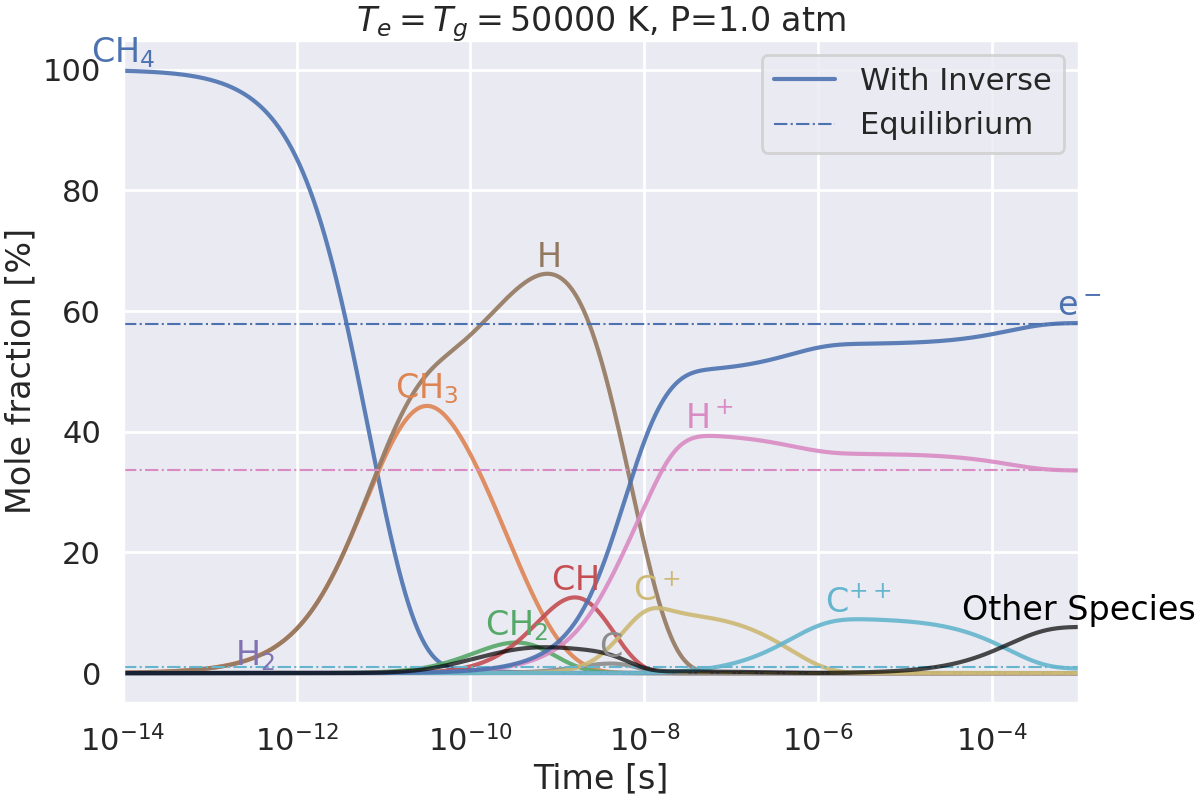
Do we get the same equilibrium with and without inverse reactions?#
This example checks if the equilibrium of two mechanisms is the same:
one with inverse reactions,
one without inverse reactions.
Key formula used for reverse rate constant calculation:
\[k_b = \frac{k_f}{K_{eq}}\]
where:
\(k_b\): backward rate constant
\(k_f\): forward rate constant
\(K_{eq}\): equilibrium constant
The equilibrium constant is computed from Gibbs free energy:
\[K_{eq} = \exp\left(-\frac{\Delta G}{R T}\right)\]
where:
\(\Delta G\): Gibbs free energy change
\(R\): universal gas constant
\(T\): temperature
For two-temperature plasma reactions, in equilibrium, the electron temperature is equal to the gas temperature, and the rate constant is computed using the above formula.
# This is an option for the online documentation, so that each image is displayed separately.
# sphinx_gallery_multi_image = "single"
Import the required libraries.#
import cantera as ct
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from rizer.misc.utils import get_path_to_data
sns.set_theme("poster")
Define the mechanism and parameters.#
mechanism_no_inverse = get_path_to_data(
"mechanisms",
"Goutier2025",
"builder",
"5_CH4_to_C2H2_forward_reactions.yaml",
)
mechanism_with_inverse = get_path_to_data(
"mechanisms",
"Goutier2025",
"CH4_to_C2H2.yaml",
)
# Temperatures in Kelvin
temperatures_no_inverse = [
5000,
10000,
15000,
] # Cannot go higher than 15000 K
temperatures_with_inverse = [
5000,
10000,
15000,
20000,
30000,
40000,
50000,
] # Not limited
P = ct.one_atm
X_ini = {"CH4": 1}
species_to_plot = [
"CH4",
"CH3",
"CH2",
"CH",
"H2",
"H",
"H+",
"C",
"C+",
"C++",
"e-",
]
label_latex = {
"CH4": r"$\mathregular{CH_4}$",
"CH3": r"$\mathregular{CH_3}$",
"CH2": r"$\mathregular{CH_2}$",
"CH": r"$\mathregular{CH}$",
"H2": r"$\mathregular{H_2}$",
"H": r"$\mathregular{H}$",
"H+": r"$\mathregular{H^+}$",
"C": r"$\mathregular{C}$",
"C+": r"$\mathregular{C^+}$",
"C++": r"$\mathregular{C^{++}}$",
"e-": r"$\mathregular{e^-}$",
}
# Initialize a storage dictionary to hold the results.
# Key and values:
# {"temperature":
# { "time": [...], "species1": [...], "species1_eq": ..., "species2": [...], "species2_eq": ... }
# }
storage_dict_no_inverse: dict[int, dict[str, list[float]]] = {}
storage_dict_with_inverse: dict[int, dict[str, list[float]]] = {}
storage_dict_eq: dict[int, dict[str, float]] = {}
for temperature in temperatures_no_inverse:
storage_dict_no_inverse[temperature] = {}
storage_dict_no_inverse[temperature]["time_no_inverse"] = []
for species in species_to_plot:
storage_dict_no_inverse[temperature][f"{species}_no_inverse"] = []
for temperature in temperatures_with_inverse:
storage_dict_with_inverse[temperature] = {}
storage_dict_with_inverse[temperature]["time_with_inverse"] = []
for species in species_to_plot:
storage_dict_with_inverse[temperature][f"{species}_with_inverse"] = []
for temperature in temperatures_with_inverse:
storage_dict_eq[temperature] = {}
for species in species_to_plot:
storage_dict_eq[temperature][f"{species}_eq"] = 0.0
# Parameters for the reactor network.
simulation_time = 1e-3 # Simulation time in seconds
rtol = 1e-8 # Relative tolerance for the reactor network
max_steps = 100_000 # Maximum steps for the reactor network
max_time_step = 1e-7 # Maximum time step for the reactor network
gas_no_inverse = ct.Solution(mechanism_no_inverse, name="gas")
gas_with_inverse = ct.Solution(mechanism_with_inverse, name="gas")
Run the equilibrium calculations.#
# ----- Calculate the equilibrium for the mechanism without inverse reactions. ----- #
for T in temperatures_no_inverse:
print(f"Running equilibrium for T={T} K")
# Use a reactor network and advance to equilibrium.
gas_no_inverse.TPX = T, P, X_ini
r1 = ct.IdealGasConstPressureReactor(gas_no_inverse, energy="off")
sim = ct.ReactorNet([r1])
sim.rtol = rtol # Set relative tolerance for the reactor network.
sim.max_time_step = max_time_step
sim.reinitialize()
# Store the states in a SolutionArray.
states_no_inverse = ct.SolutionArray(gas_no_inverse, 1, extra={"t": [0.0]})
i = 0 # Initialize a counter for the number of steps.
while sim.time < simulation_time:
# Advance the reactor network by one step.
sim.step()
# Append the current state to the SolutionArray.
states_no_inverse.append(gas_no_inverse.state, t=sim.time)
if i % 1000 == 0:
print(f"Time: {sim.time:.2e} s")
i += 1
# Store the results in the dictionary.
storage_dict_no_inverse[T]["time_no_inverse"] = states_no_inverse.t # type: ignore
for species in species_to_plot:
storage_dict_no_inverse[T][f"{species}_no_inverse"] = (
states_no_inverse(species).X * 100
)
# ----- Calculate the equilibrium for the mechanism with inverse reactions. ---- #
for T in temperatures_with_inverse:
print(f"Running equilibrium for T={T} K")
gas_with_inverse.TPX = T, P, X_ini
initial_X = gas_with_inverse.X.copy()
# Equilibrate at constant T and P (reference equilibrium)
gas_with_inverse.equilibrate(
"TP",
solver="auto",
rtol=rtol,
max_steps=max_steps,
# max_iter=100, # This is only relevant if a property pair other than (T,P) is specified.
estimate_equil=0,
log_level=0,
)
equil_X = gas_with_inverse.X.copy()
# Use a reactor network and advance to equilibrium
gas_with_inverse.TPX = T, P, X_ini
r2 = ct.IdealGasConstPressureReactor(gas_with_inverse, energy="off")
sim = ct.ReactorNet([r2])
sim.rtol = rtol # Set relative tolerance for the reactor network
sim.max_time_step = max_time_step
sim.reinitialize()
# Store the states in a SolutionArray.
states_with_inverse = ct.SolutionArray(gas_with_inverse, 1, extra={"time": [0.0]})
i = 0 # Initialize a counter for the number of steps.
while sim.time < simulation_time:
# Advance the reactor network by one step.
sim.step()
# Append the current state to the SolutionArray.
states_with_inverse.append(gas_with_inverse.state, time=sim.time)
if i % 1000 == 0:
print(f"Time: {sim.time:.2e} s")
i += 1
# Store the results in the dictionary.
storage_dict_with_inverse[T]["time_with_inverse"] = states_with_inverse.time # type: ignore
for species in species_to_plot:
storage_dict_eq[T][f"{species}_eq"] = (
equil_X[gas_with_inverse.species_index(species)] * 100
)
storage_dict_with_inverse[T][f"{species}_with_inverse"] = (
states_with_inverse(species).X * 100
)
Running equilibrium for T=5000 K
/home/runner/work/rizer/rizer/examples/kinetics/plot_equilibrium_reverse_reaction.py:166: DeprecationWarning: ReactorBase.__init__: After Cantera 3.2, the default value of the `clone` argument will be `True`, resulting in an independent copy of the `phase` being created for use by this reactor. Add the `clone=False` argument to retain the old behavior of sharing `Solution` objects.
r1 = ct.IdealGasConstPressureReactor(gas_no_inverse, energy="off")
Time: 3.28e-19 s
Time: 1.64e-05 s
Time: 1.16e-04 s
Time: 2.16e-04 s
Time: 3.16e-04 s
Time: 4.16e-04 s
Time: 5.16e-04 s
Time: 6.16e-04 s
Time: 7.16e-04 s
Time: 8.16e-04 s
Time: 9.16e-04 s
Running equilibrium for T=10000 K
Time: 4.72e-20 s
Time: 1.34e-06 s
Time: 8.41e-05 s
Time: 1.84e-04 s
Time: 2.84e-04 s
Time: 3.84e-04 s
Time: 4.84e-04 s
Time: 5.84e-04 s
Time: 6.84e-04 s
Time: 7.84e-04 s
Time: 8.84e-04 s
Time: 9.84e-04 s
Running equilibrium for T=15000 K
Time: 2.70e-20 s
Time: 1.15e-06 s
Time: 8.20e-05 s
Time: 1.82e-04 s
Time: 2.50e-04 s
Time: 3.50e-04 s
Time: 4.50e-04 s
Time: 5.50e-04 s
Time: 6.50e-04 s
Time: 7.50e-04 s
Time: 8.50e-04 s
Time: 9.50e-04 s
Running equilibrium for T=5000 K
/home/runner/work/rizer/rizer/examples/kinetics/plot_equilibrium_reverse_reaction.py:214: DeprecationWarning: ReactorBase.__init__: After Cantera 3.2, the default value of the `clone` argument will be `True`, resulting in an independent copy of the `phase` being created for use by this reactor. Add the `clone=False` argument to retain the old behavior of sharing `Solution` objects.
r2 = ct.IdealGasConstPressureReactor(gas_with_inverse, energy="off")
Time: 3.28e-19 s
Time: 1.39e-05 s
Time: 1.14e-04 s
Time: 2.14e-04 s
Time: 3.14e-04 s
Time: 4.14e-04 s
Time: 5.14e-04 s
Time: 6.14e-04 s
Time: 7.14e-04 s
Time: 8.14e-04 s
Time: 9.14e-04 s
Running equilibrium for T=10000 K
Time: 4.72e-20 s
Time: 1.39e-06 s
Time: 6.17e-05 s
Time: 1.62e-04 s
Time: 2.62e-04 s
Time: 3.62e-04 s
Time: 4.62e-04 s
Time: 5.62e-04 s
Time: 6.62e-04 s
Time: 7.62e-04 s
Time: 8.62e-04 s
Time: 9.62e-04 s
Running equilibrium for T=15000 K
Time: 2.70e-20 s
Time: 5.19e-07 s
Time: 2.07e-05 s
Time: 1.21e-04 s
Time: 2.21e-04 s
Time: 3.21e-04 s
Time: 4.21e-04 s
Time: 5.21e-04 s
Time: 6.21e-04 s
Time: 7.21e-04 s
Time: 8.21e-04 s
Time: 9.21e-04 s
Running equilibrium for T=20000 K
Time: 2.13e-20 s
Time: 1.86e-07 s
Time: 3.37e-05 s
Time: 1.34e-04 s
Time: 2.34e-04 s
Time: 3.34e-04 s
Time: 4.34e-04 s
Time: 5.34e-04 s
Time: 6.34e-04 s
Time: 7.34e-04 s
Time: 8.34e-04 s
Time: 9.34e-04 s
Running equilibrium for T=30000 K
Time: 1.78e-20 s
Time: 4.83e-09 s
Time: 1.65e-06 s
Time: 9.75e-05 s
Time: 1.98e-04 s
Time: 2.98e-04 s
Time: 3.98e-04 s
Time: 4.98e-04 s
Time: 5.98e-04 s
Time: 6.98e-04 s
Time: 7.98e-04 s
Time: 8.98e-04 s
Time: 9.98e-04 s
Running equilibrium for T=40000 K
Time: 1.70e-20 s
Time: 2.13e-09 s
Time: 5.57e-08 s
Time: 4.95e-05 s
Time: 1.50e-04 s
Time: 2.50e-04 s
Time: 3.50e-04 s
Time: 4.50e-04 s
Time: 5.50e-04 s
Time: 6.50e-04 s
Time: 7.50e-04 s
Time: 8.50e-04 s
Time: 9.50e-04 s
Running equilibrium for T=50000 K
Time: 1.70e-20 s
Time: 1.82e-09 s
Time: 3.16e-08 s
Time: 4.74e-05 s
Time: 1.47e-04 s
Time: 2.47e-04 s
Time: 3.47e-04 s
Time: 4.47e-04 s
Time: 5.47e-04 s
Time: 6.47e-04 s
Time: 7.47e-04 s
Time: 8.47e-04 s
Time: 9.47e-04 s
Merge the results from both mechanisms.#
storage_dict: dict[int, dict[str, list[float]]] = {}
for T in temperatures_no_inverse:
# Add the results from the no inverse mechanism.
storage_dict[T] = storage_dict_no_inverse[T].copy()
for T in temperatures_with_inverse:
if T in storage_dict:
# If the temperature is already in the dictionary, we merge the results.
storage_dict[T].update(storage_dict_with_inverse[T])
else:
# If the temperature is not in the dictionary, we add it.
storage_dict[T] = storage_dict_with_inverse[T].copy()
temperatures = sorted(storage_dict.keys())
Plotting the results.#
for T in temperatures:
print(f"Plotting results for T={T} K")
fig, ax = plt.subplots(figsize=(12, 8), layout="constrained")
other_species = np.ones_like(storage_dict[T]["time_with_inverse"]) * 100.0
print(other_species.shape)
for species in species_to_plot:
# Plot the time evolution of the mole fraction, with inverse reactions.
x = np.array(storage_dict[T]["time_with_inverse"])
y = np.array(storage_dict[T][f"{species}_with_inverse"])
other_species -= y[:, 0]
(line_with_inverse,) = ax.plot(
x,
y,
label=f"{species} (With Inverse)",
linestyle="-",
alpha=0.9,
)
# Add the species name at the maximum point, with the same color as the line.
max_x = x[y.argmax()]
if max_x < 1e-14:
max_x = 1e-14
max_y = y.max()
ax.text(
x=max_x,
y=max_y,
s=label_latex[species],
color=ax.lines[-1].get_color(),
fontsize=24,
ha="center",
va="bottom",
)
# Plot the equilibrium value as a horizontal line.
line_eq = ax.axhline(
storage_dict_eq[T][f"{species}_eq"],
color=ax.lines[-1].get_color(),
linestyle="-.",
linewidth=1.5,
)
# Plot the no inverse results, if available.
if "time_no_inverse" in storage_dict[T]:
(line_without_inverse,) = ax.plot(
storage_dict[T]["time_no_inverse"],
storage_dict[T][f"{species}_no_inverse"],
label=f"{species} (No Inverse)",
linestyle="--",
alpha=0.5,
color=ax.lines[-1].get_color(),
)
# Plot the remaining species as "Other Species"
(line_other_species,) = ax.plot(
storage_dict[T]["time_with_inverse"],
other_species,
label="Other Species (With Inverse)",
linestyle="-",
alpha=0.7,
color="black",
)
# Add the species name at the maximum point, with the same color as the line.
max_x = storage_dict[T]["time_with_inverse"][np.argmax(other_species)]
if max_x < 1e-14:
max_x = 1e-14
max_y = np.max(other_species)
ax.text(
x=max_x,
y=max_y,
s="Other Species",
color=ax.lines[-1].get_color(),
fontsize=24,
ha="center",
va="bottom",
)
ax.set_xlabel("Time [s]")
ax.set_xscale("log")
ax.set_xlim(left=1e-14, right=simulation_time)
ax.set_ylabel("Mole fraction [%]")
ax.set_title(f"$T_e=T_g={T}$ K, P={int(P / ct.one_atm):.1f} atm")
# Add legend
if "time_no_inverse" in storage_dict[T]:
ax.legend(
[line_with_inverse, line_eq, line_without_inverse],
["With Inverse", "Equilibrium", "No Inverse"],
)
else:
ax.legend(
[line_with_inverse, line_eq],
["With Inverse", "Equilibrium"],
)
plt.show()
Plotting results for T=5000 K
(10863,)
Plotting results for T=10000 K
(11385,)
Plotting results for T=15000 K
(11795,)
Plotting results for T=20000 K
(11666,)
Plotting results for T=30000 K
(12027,)
Plotting results for T=40000 K
(12507,)
Plotting results for T=50000 K
(12528,)
Total running time of the script: (0 minutes 11.883 seconds)