—

Analysis of Philippe Castera’s circuit.

Reproducing the results of Philippe Castera’s thesis [Castera2015].

The circuit solved is the following (see figure 4.2.1 in [Castera2015]):

 ┌-------------------(L-L_p)------┐
 │       ↑  │                     │
 │      u_c C                    L_p
R_b      │  │                     │
 │         R_sg                  R_p(t)
 │          │                     │
 ┖--------------------------------┘

where:

• \(C\) is the capacitance of the capacitor,

• \(R_b\) is the resistance of the ballast resistor,

• \(R_sg\) models the wires and sparkgap resistances,

• \(R_p(t)\) is the time-varying resistance of the plasma,

• \(L_p\) is the stray inductance related to the plasma channel and the wiring between the connection points of the voltage probe.

The plasma resistance is modeled here by following the Rompe-Weizel model:

\[R_p^{RW}(t) = \frac{k^{RW} l}{\left(\int_{-\infty}^t i_p^2(t) d t\right)^{\frac{1}{2}}}, \quad k^{RW}=\left(\frac{\frac{3}{2} k_B T_{e}+e \phi_I}{2 \mu_{e} e}\right)^{\frac{1}{2}}\]

Tags: electric circuit validation time-varying resistance Castera Rompe-Weizel Vlastos Braginskii

Import the required libraries.

import seaborn as sns

from tests.electric_circuit.test_castera_circuit import test_fig4_2_2, test_fig_4_3_1

sns.set_theme("poster")

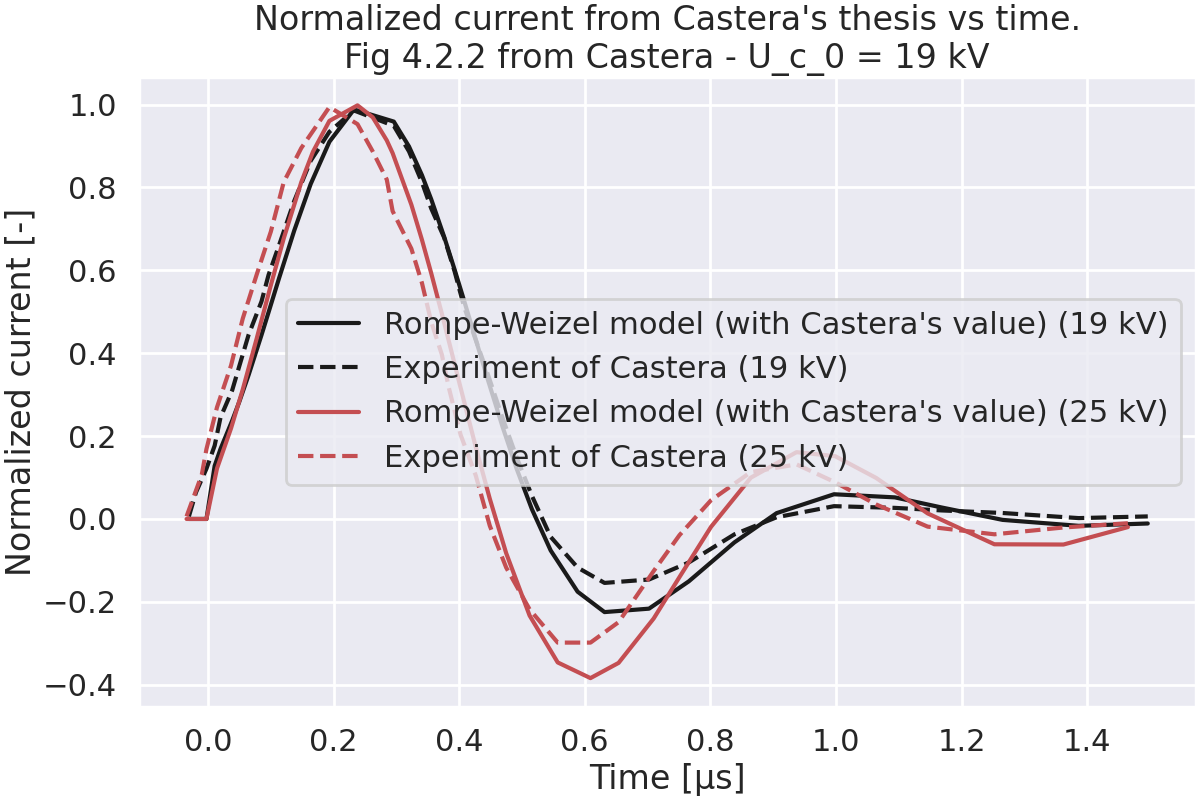
Plot figure 4.2.2.

test_fig4_2_2(plot=True)

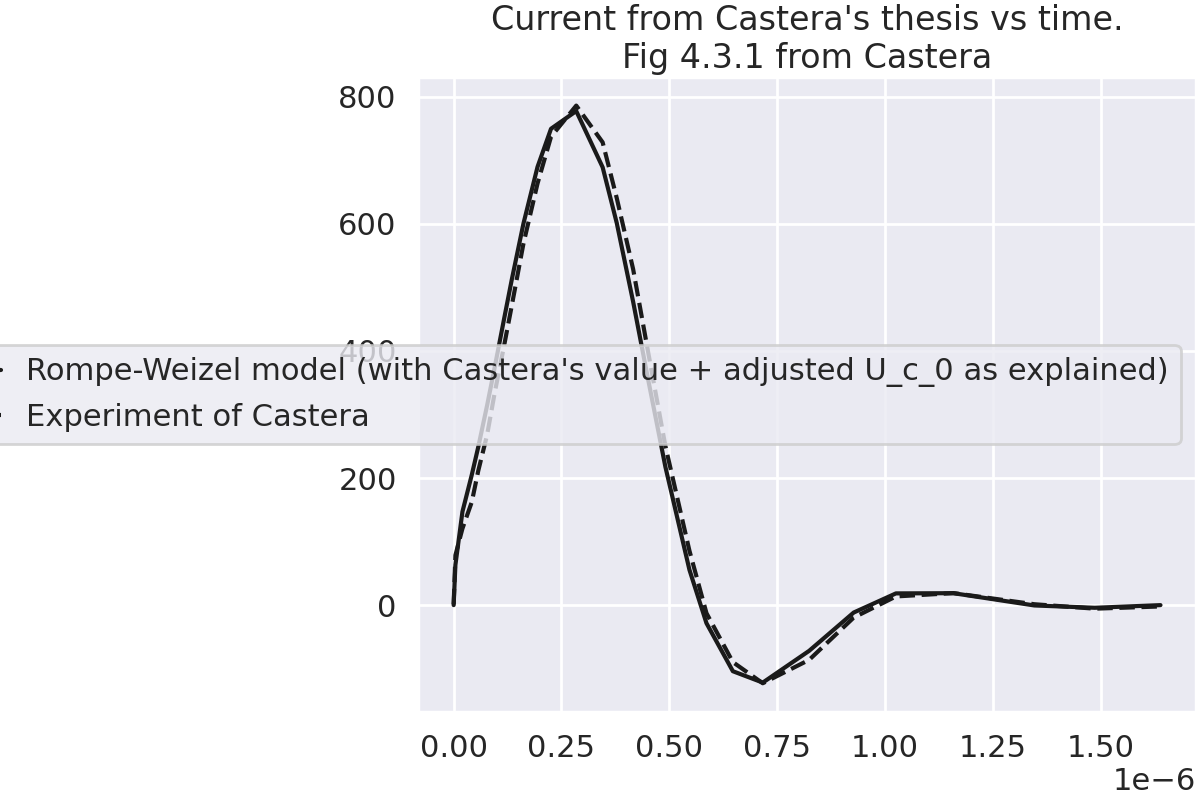
Plot figure 4.3.1.

test_fig_4_3_1(plot=True)